유사전공자
01. 에너지 밴드(Energy band)의 형성 과정 본문
#0. 에너지 밴드를 알기 위해서
양자역학에서, 구속된 전자는 양자화된(불연속적인) energy를 가진다고 배웠다.
에너지 밴드를 알기 위해 하나 더 필수적으로 알아야 할 것은, 바로 파울리 배타원리이다.
< Pauli Exclusion Principal >
전자가 오비탈에 배치될 때 네 가지 양자수가 모두 같은 전자쌍은 존재할 수 없다.
이 원리에 따르면 하나의 orbital에는 최대 2개의 electron이 배치되며, 이때 두 electron의 spin direction은 서로 다르다.
따라서 orbital에 배치 될 수 있는 electron의 최대 수는 s orbital이 2개, p orbital은 6개, d orbital이 10개이다.
파울리 배타원리에는 다양한 관점에서만큼 다양한 설명이 있지만, 우리가 가장 중요하게 생각해야 할 것은
" 같은 원자가 인접하게 되면 원리에 따라 전자의 에너지 준위가 분리된다 "
이 원리를 가지고 에너지 밴드가 무엇인지 알아봅시다.
#1. 에너지 밴드
원자에 포함되어 있는 전자가 갖고 있는 에너지는 불연속적인 값을 갖고 있다고 하였다.
두 원자가 인접하여 최외각 에너지 전자의 전자궤도가 공간적으로 중첩된다면, 파울리 배타 원리에 의해 전자가 서로 분리되게 되는데, 이때 전자가 갖고 있는 에너지 준위 또한 분리되게 된다.
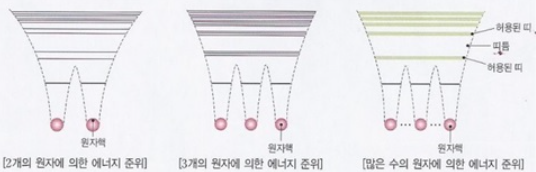
무수히 많은 원자가 인접하게 될 때, 무수히 많은 에너지 준위 또한 각각 분리되어야 하고, 무수히 많은 중첩이 발생하여
마치 연속된 띠 모양의 준위를 형성하게 되는데, 이것이 에너지 밴드.

위 그림과 같이 우리가 에너지 밴드를 생각할때 떠올리는 그림은, 다음 게시물에 설명할 예정이다.
다양한 경우에서의 에너지 밴드 형성과정을 알아보자.
#2. 에너지 밴드의 형성 과정
a. 다중전자 원자의 경우(일반적인 경우)
원자들이 인접하는 경우에,
- 최외각 전자로부터 순차적으로 전자궤도 중첩 발생
- 전자 각각의 에너지 준위가 중첩원리에 의해 분리되어 에너지밴드 형성
- 기존 불연속 에너지 준위 간의 에너지 간격으로 인해 에너지 밴드간에 전자가 가지지 못하는 에너지 간격 발생
여기서 전자가 가지지 못하는 에너지 간격이 뭘 의미할까? 라는 의문점이 생긴다.

좌측 그림과 같이, 3개의 전자궤도를 가지는 가상의 원자를 가정하자.
3개의 궤도에 있는 각 전자는 불연속적인 각각의 에너지 준위를 가지고, 각 에너지 준위마다 차이를 보이기 때문에, 전자가 가지지 못하는 에너지 간격이 발생된다.
위 설명을 그래프화 한다면

허용 에너지 밴드 : 기존 에너지 준위에서 분기하여 결정에서 전자가 가질 수 있는 에너지밴드
금지 에너지 밴드 : 기존 에너지 준위 간격에서 분기하여 결정에서 전자가 가질 수 없는 에너지 밴드
b. Si 결정의 경우
상당히 복잡한 개념이다. Si원자의 전자궤도부터 천천히 알아보도록 하자.

실리콘의 전자 개수는 14개이고, 좌측 그림처럼 n=1개는 2개, n=2개는 8개까지의 전자가 들어갈 수 있어 낮은 에너지 상태에 먼저 위치하는 전자의 성질때문에 남은 공간 없이 전부 위치하게 되었고,
남은 4개의 전자는 최외각 궤도(n=3), 즉 가장 높은 에너지 준위에 존재한다.
그림의 우측에서 확인할 수 있듯이, 최외각 전자 4개중 2개는 다른 2개의 전자보다 약간 낮은 에너지 준위에 존재한다.
(n=3는 3s궤도와 3p궤도로, 미세한 차이가 나는 두 에너지 준위가 포함되어 있다.)
Two allowed levels : 3s 궤도에는 2개의 전자가 허락된다.
Six allowed levels : 3p 궤도에는 6개의 전자가 허락된다.
이 두 궤도를 합쳐서 n=3(최외각 궤도)에는 총 8개의 전자가 존재할 수 있게 되는 것이고, 낮은 에너지 준위부터 전자가 채워지기 때문에, 3s 궤도에는 2개의 자리 중 2개 전부가 채워지고, 3p 궤도 에는 남은 2개의 전자가 위치하게 되는 것이다.
이 최외각 전자 4개만이 Si원자의 결합에 관여하는 것이다. 이제 Si의 에너지 밴드 형성 그림을 보자.

먼저, 위 그래프는 Si원자들이 원자 핵 사이 거리 r에서 단결정 격자를 이루는 경우를 나타냈으므로, 단결정 격자를 보자.

좌측 그림이 Si 단결정을 나타내고, 위 그래프의$a_0$ 가 그림의 Si 단결정의 원자간 거리 0.15nm를 의미한다.
위 그래프를 다시 보자.
앞서 설명한 것처럼, n=3 껍질 내에 포함되는 2s와 3p 궤도는 미세한 차이가 나는 서로 다른 에너지 준위이다.
Si 원자들이 서로 가까워 질 경우(위 그래프의 r 감소에 해당)
" 그래프 해석 "
1. 원자에 구속되어 있는 전자들이 중첩하며(a 구역에서 2갈래로 갈라지기 시작하는 부분) 에너지 밴드가 형성되기 시작
2. 원자 핵 사이가 거리 r이 일정 거리가 되었을 때, 3s, 3p 상태에 존재하는 전자들이 중첩되어 하나의 밴드 형성(b 구역)
3. 원자 핵 사이 거리가 $a_0$ 가 되었을 때, 밴드는 다시 분리되게 된다.(c와 d 구역)
3번처럼 분리된 에너지 밴드를 형성하였을 때, 원자간 거리가 $a_0$일때 Si 단결정을 형성하였다고 하였으므로
" c,d 구역처럼 나타나는 밴드를 Si 단결정의 에너지밴드 상태" 라고 정의한다.
'반도체 > 물성 키워드' 카테고리의 다른 글
| 06. 반도체의 도핑(doping) , extrinsic semiconductor (0) | 2022.09.27 |
|---|---|
| 05. 반도체의 캐리어 농도 (2) | 2022.09.24 |
| 04. 페르미 디락 분포확률함수(Fermi-Dirac's distribution) (0) | 2022.09.22 |
| 03. (에너지) 상태 밀도 함수 (2) | 2022.09.19 |
| 02. 에너지 밴드 다이어그램(energy band diagram) (1) | 2022.09.15 |




